物理化学公式推导

status

type

date

slug

summary

文档仅对物理化学中一些不能一眼就能推出来的公式进行推导整理，非公式汇总。如有错误或遗漏，请在下方留言。

热力学

热力学第一定律：

焓变定义式：

等容过程的焓变：

当时，

等压过程的焓变：

当时，

当用和表示时，要加上等温的条件，因为化学反应一定是在确定的温度下讨论的。

热力学能变和焓变计算公式

对于无相变、化学反应和非体积功的系统定义热容：

如恒容无非体积功，有，于是有恒容摩尔热容：

移项取积分，将Cv当成常数有：

同理，如恒压无非体积功，有恒压摩尔热容：移向取积分，将Cp当成常数有：

上面两条式子适用于：
任意物质，无化学反应无相变（单组份单相体系）的恒容过程或恒压过程，无需无非体积功的条件，因为有无非体积功不影响状态函数ΔU和ΔT的关系，影响的是Q值。
理想气体的任意pVT变化过程，因为理想气体的U和H只与温度有关。

等温可逆过程的功和热

由1.1可知等温过程ΔU = ΔH = 0，于是由功的定义式与理想气体状态方程有：

绝热可逆方程式

由热力学第一定律可知，绝热Q = 0，有：

将定义为热容比。又（具体见热力学基本方程推导），有：

于是有，将T或V用理想气体状态方程替换，即可得到和。

绝热过程的功或多方过程的功

对于绝热过程，Q = 0，W = ΔU，有：

对于多方过程pVn = C，因为介于恒温可逆与绝热可逆之间，用功的定义式有：

多方过程要求.事实上，绝热过程的功也能从这条定义式推出来，可以看出两者有相同的形式。凡是能写成这种形式的气体状态方程都可以用这条式子算功，比如恒温可逆过程有，的过程可以写成,虽然不是多方过程，但也能套用此公式。

求焦-汤系数①

求焦-汤系数有两种方法，在此先用热力学第一定律及全微分方法，也是天大教材上的方法。另一种方法放到热力学基本方程。

对于任意气体，有：，展开为全微分有：

对于节流膨胀，有：；

卡诺热机效率及推论

卡诺循环分为四个步骤，两个等温可逆，两个绝热可逆。对于一个热机的效率定义为。具体到卡诺热机有。

由绝热可逆方程式：或理想气体熵变公式，可求出，于是有：

将和带入，有：

由，可推导出推论和。

无论卡诺热机正开还是倒开都有这个推论，对于冷冻机；对于热泵。注意只有当过程可逆时才有：，不可逆时只有：。注意的是。这条式子里面的都是相对于人的视角来说的，人得到了功是，失去了热是。

克劳修斯不等式推导

由卡诺定理可知，，于是有：

当可逆时取＝号，此时就是熵变的定义式；不可逆时取＜号。

构建一个不可逆循环，由一段可逆过程和一段不可逆过程组成，有：

可以看到不等式左侧是可逆过程的热温商，根据定义其就是熵变，有：

当可逆时取=号，不可逆时取<号。

亥姆霍兹函数和吉布斯函数判据推导

亥姆霍兹函数判据

由克劳修斯不等式可知，等温时有:

若等温的同时恒容有，若等温恒容且无非体积功有：

吉布斯函数判据

同样由克劳修斯不等式，等温时有，当等压时有：

当等温等压无非体积功时有：

注意：虽然推导的时候用到了无非体积功，但使用这两个判据时并不需要无非体积功这个条件。因为一个过程是否自发是这个过程本身的趋势，和有无非体积功无关，只有判断过程是否可逆时才需要看有无非体积功（因为此时是判断具体的过程）。

热力学基本方程及推论

由可逆过程的热温商，可逆过程的体积功及互算关系可得出热力学基本方程：

适用于单组分单相体系的任意pVT过程或多组分多相体系没有非体积功的可逆过程。真实气体也适用。

推论一

从上面四条基本方程我们可以很轻易的得出如下结论：

推论二——麦克斯韦关系式

推导麦克斯韦关系式的核心是多元函数交换求导顺序结果不变，由热力学基本方程和推论一可得

其余三条式子也用同样的方法求出。

证明吉布斯-亥姆霍兹函方程

根据商规则，令，有：

同理可得：

热容关系式

由等容热容定义式，热力学基本方程可知，等容时有，，代入可得：

同理，等压时，有：

和关系式证明

由等容摩尔热容和等压摩尔热容定义式有：

写出U(TV)或U(Tp)的全微分，一般来说和U, A对应写成与V有关的形式更方便。

两边在压力不变的情况下，同时除以，有：

将此式带入，化简得：

求焦-汤系数②

写出H(pT)的全微分并令其等于0：

移项整理，可得：

证明钢球模型的U只是T的函数

对于钢球模型：，可以固定温度，看热力学能随压力或体积的变化率。

质量摩尔浓度的计算公式

质量摩尔浓度bB的定义式：，单位为mol/kg，所以要在分子×1000。

加和公式推导

偏摩尔量定义为。物理意义为：在有限的体系中加入摩尔的组分B（因为是微小量所以组成未变）引起的体系广度量的改变，折合成1mol组分B时的改变量。

写出任意广度量的全微分:

为方便起见，令表示所有组分的物质的量都保持不变，表示除了B组分外其余组分的物质的量保持不变。将的定义式带入，有：

在等温等压时，对上式两端取积分，有：两边同时除以物质的量有：

吉布斯-杜亥姆公式推导

对加和公式两端求导有：

在T, p一定时，由dX的全微分可知：

两式相比，可得当T, p一定时：

对于两组分体系有：

理想液态混合物的化学势推导

方法一

由化学势判据，液体和其平衡蒸汽化学势相同，有：

由理想气体化学势表达式有：

将拉乌尔定律pB = pB*xB代入：

方法二

第一步同上，标准态不再采用100kpa，而是采用饱和蒸汽的压力：

稀溶液的依数性

蒸汽压下降

由拉乌尔定律：

有此式可直观看出稀溶液的依数性，代表着溶剂的性质，代表溶质的数量。

凝固点降低

因为只有析出固体为纯溶剂时，才有凝固点降低，所以凝固时，有溶剂的化学势等于固体的化学势，设与温度无关：

设计过程：

溶液中溶剂→纯溶剂

纯溶剂μ(T)→纯固体μ(T):

所以，总的化学势变化有：

整理，得：

此式是最一般的凝固点降低公式，可适用于理想液态混合物。且与沸点升高公式，克拉佩龙方程（温度对相平衡压力的影响），范特霍夫方程（温度对平衡常数的影响）和阿伦尼乌斯公式（温度对速率常数的影响）形式相同。

下面通过三个近似，继续推导更特殊的凝固点降低公式：

因为是稀溶液，≈ 0，当x_B → 0时，。

因为是稀溶液，

，因为凝固点降低不可能降低太多，而正常凝固点都高达1，200k，所以可以近似。

带入一般式得：

注意此式不再适用于理想液态混合物，因为第一步近似要求溶液必须是数学意义上的稀溶液，而理想液态混合物因为全程满足拉乌尔定律和亨利定律，所以可以看成理想稀溶液，这是因为理想液态混合物两组分性质差距不大所导致的，但这不是真正的稀溶液。

沸点升高

与凝固点降低推导类似，只有溶质不挥发，才有沸点升高，有：

渗透压

渗透压公式推导的核心思想是半透膜两侧的溶液和纯溶剂化学势要相等，因为压力会影响化学势，实际上溶液这边的化学势，靠上升的一段液柱的流体静压力来平衡纯溶剂的化学势，有

由热力学基本方程可知，等温时：

对此式做定积分：

在压力不太大的情况下，可以看作常数，有：

将此式带回第一条式子，对比可得：

因为是稀溶液，所以有；有：

克拉佩龙方程推导

对于一个可逆相变(α−β)过程，在温度T下的饱和蒸汽压是p，在温度T + dp下的饱和蒸汽压为p + dp，由于都是可逆相变所以ΔG = 0。因此有α相从T, p变到T + dT, p + dp过程的与β相从T, p变到T + dT, p + dp过程的相等。

对于液固相变，将上式改写为：

因为压力对凝聚态体系的影响非常小，所以ΔfusVm, ΔfusHm都近似看为常数。积分得：

克克方程推导

由克拉佩龙方程：

因为液体体积与气体相比很小，忽略不计，气体看作理想气体所以有:

带回有：

做定积分有：

化学反应等温式推导

由加和公式，将代入有：

把理想气体化学势表达式代入上式：

当化学反应达到平衡时，，有：

范特霍夫方程推导

由吉布斯-亥姆霍兹方程，将平衡时的代入得：

取定积分有：

范特霍夫方程推论

由:

取对数：

因为都是与温度无关的常数，所以第二项为0，有：

代入范特霍夫方程：

动力学

反应速率

转化速率的定义式为：

反应速率的定义式为：

对于一个化学反应：，反应速率可以表示为：

n级反应速率方程

微分形式：

导出积分式：

证明kp与kc的关系

由理想气体状态方程可得，代入反应速率方程：

证明

对于任意恒容基元反应：aA + bB = cC，达到平衡时正逆反应速率相同，有：

因为反应的平衡常数所以有：

由范特霍夫方程推论和阿伦尼乌斯公式，有：

电化学

证明离子迁移数

由法拉第定律Q = zFξ，当反应进度ξ = 1时，有Q = zFn。

对正离子有：

由于溶液是电中性的，有：，都是常数，所以有：

又因为迁移率和电迁移率之间有：，所以有：

证明摩尔电导率和电迁移率的关系

由摩尔电导率定义式：

原电池热力学

对于可逆电池有：

证明酸性条件的氢电极与碱性条件的氢电极电极电势之差为0.828V

对于一个电池：

因为，推导电动势有：

由此可见酸性和碱性条件下的氢电极电势相差了0.828V，对于氧电极也有相同的结论。

界面化学

杨-拉普拉斯方程推导

压强的定义式为Δp = F/S

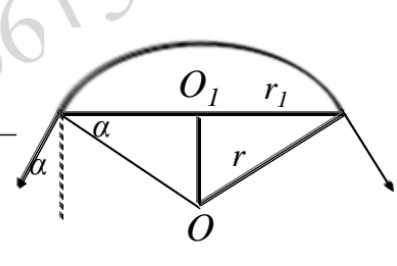
对于一个弯曲液面，其表面张力在水平方向上相互抵消，在竖直方向上有一个合力F = 2πr1γcosα，代入压强定义式有：

对于一个椭球体通常有两个曲率半径，所以上式可化为：

对于毛细现象，液面上升高度有：

式中，为毛细管半径，α为接触角。

开尔文公式推导

假设在一定温度下平液面的饱和蒸汽压为p，弯曲液面的饱和蒸汽压为。

对于凸液面，由理想气体的化学势表达式，有：

对于液体有

将杨-拉普拉斯方程代入，有：

平衡时两边化学势变化量相等，有：

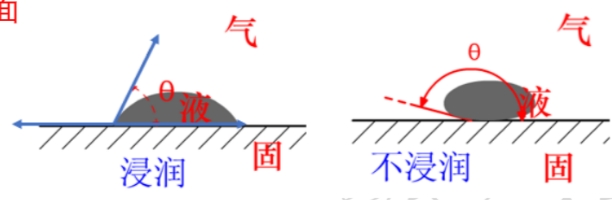
杨氏方程推导

对于一个液固界面，有：

朗缪尔吸附等温式推导

朗缪尔吸附有四个要点：

单分子层吸附

固体表面均匀

被吸附在固体表面上的分子间无作用力

吸附平衡是动态平衡

设固体表面有N个点位，覆盖率为θ，那么已经吸附气体分子的点位为N * θ，没被吸附的点位为N(1−θ)。

对于一个化学反应：

其速率方程有：

定义吸附强度

得出：

胶体化学

胶体粒子在重力场中的分布

由亥姆霍兹函数判据可知ΔA = W，对于重力场中的分子有：

对于离心场，将g替换为离心加速度，将代入